机器人达到指定位置方法数
问题概述:动态规划的题目,假设有N个位置,N大于等于2。开始机器人在其中的某个位置(M位置,M一定是1到N的某一个),机器人可以往左走或往右走,在位置1则只能往右走到位置2,同理在位置N只能往左走到N-1位置。在除了这两个位置的其它位置则可以往左或往右;规定机器人走K步,最终能来到P位置(P也是1到N位置中的一个)的方法有多少种,给定四个参数N、M、K、P,返回方法数。
暴力递归的方法
分析:各个参数的意义:
N:位置1 ~ N,是固定参数
cur:当前位置cur,可变参数
rest:还剩rest步没走,可变参数
P:最终的目标位置,固定参数
walk方法:
1 | public static int walk (int N,int cur,int rest,int p) { |
主方法:
1 | public static int ways1 (int N,int M,int K,int P) { |
可以在mian方法里这样调用:
1 | int N = 6,M = 1,K = 8,P = 3; |
动态规划的方法
时间复杂度:O(N * K)
从暴力递归的方法来优化成动态规划,在这个过程中,一旦写出了尝试函数,后续的优化过程都是很固定的。
这个例子中,首先根据walk方法的含义结合题意,分析整个过程是不是无后效性的。利用尝试方法去解决的问题,绝大多数都是无后效性的,有后效性的递归过程在面试过程中极其少见。所谓无后效性,就是指一个递归状态的返回值与怎么达到这个状态的路径无关。
本题中的walk函数N、P,任何时候都不变,说明N、P与具体的递归状态无关,忽略他们。只需要关注cur和rest两个参数,也就是当前来到的位置和剩余的步数。walk(cur,rest)的含义是:当前来到cur位置,还剩下rest位置可以走,那么有多少种方法走到目标P位置。例如walk(5,7),代表来到5位置,还可以走7步,最终到达P有多少种方式,如下图画出了求出walk(5,7)状态的依赖树: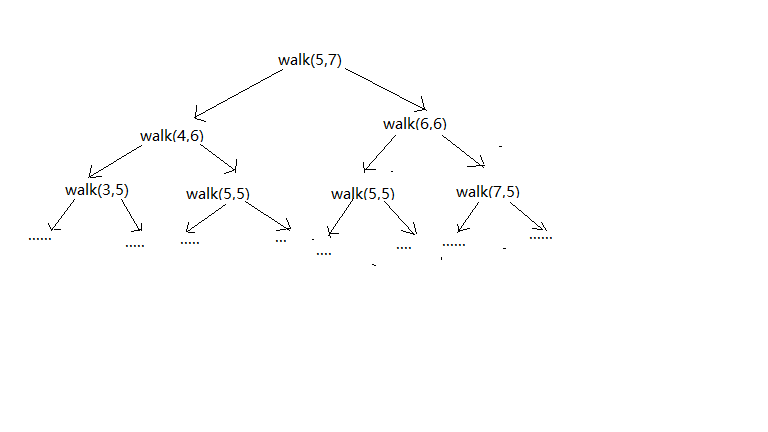
上图walk(5,5)状态出现了两次,含义是当前来到5位置,还剩5步,有效方法有多少种。那么最终的返回值与怎么到达这个状态的路径有关系吗?没有。不管是从walk(4,6)来到walk(5,5)还是从walk(6,6)来到walk(5,5),只要是”当前来到5位置,还剩5步”这个问题,返回值都是不变的,这就是一个无后效性问题。一旦问题经论证是无后效性的就可以按一下步骤进行优化成动态规划:
- 1,找到什么可变参数可以代表一个递归状态,也就是哪些参数一旦确定,返回值就确定了
- 2,把可变参数的所有组合映射成一张表,有1个可变参数就是1维表,2个就是二维表,依此类推
- 3,最终答案要的是表中的哪个位置,在表中标出
- 4,根据递归过程的base case,把这张表最简单、不需要依赖其他位置的那些位置填好值
- 5,根据递归过程非base case的部分,也就是分析表中的普遍位置需要怎么计算得到,那么这张表的填写顺序也就确定了
- 6,填好表,返回最终答案填在表中位置的值
接下来我们以N = 7,M = 4,K = 9,P = 5 为例来走一下这个过程。
过程:
1,walk函数中,可变参数cur和rest一旦确定,返回值就确定了
3,N = 7,M = 4,K = 9, P = 5的最终答案,就是dp[9][4]的值
4,递归过程的base case是指问题规模小到什么程度,就不需要再划分子问题,答案就可以直接得到了。walk函数的base case如下:
1
if (rest == 0) { return cur == P ? 1 : 0 }。
当rest = 0,cur = pP,返回1,否则返回0,本例中P = 5,所以可以把表中的第一行填好,表中的第一行所有状态都是最简单且不需要依赖其他位置的。
5,base case之外的位置,在walk函数如下:
1
2
3
4
5
6
7if (cur == 1) {
return walk(N,2,rest - 1,p);
}
if (cur == N) {
return walk(N, N - 1, rest - 1, p);
}
return walk(N,cur + 1,rest - 1, p) + walk(N,cur - 1,rest - 1, p);若cur在1位置,最终返回dp[rest][cur] = dp[rest - 1][2],若在N位置,最终返回值dp[rest][cur] = dp[rest - 1][N - 1],若cur在中间位置,dp[rest][cur] = dp[rest - 1][cur - 1] + dp[rest - 1][cur + 1]。
说明每一行的值都仅仅依赖上一行的值,那么有了上一行的值,就可以推出整张表整张表的值如下所示。6,返回dp[9][4],结果为116
动态规划方法实现代码:
1 | public static int ways2 (int N,int M,int K,int P) { |
动态规划+空间压缩的方法
与最短路径和的空间压缩技巧一样,这就是动态规划 + 空间压缩的方法。
代码如下:
1 | public static int ways3 (int N,int M,int K,int P) { |
